Como la mayoría de vosotros ya sabréis Alicia decrece y crece a lo largo de la aventura y eso es correspondiente a una función que regula su estatura (y) con respecto a una regla que define su siguiente tamaño Así que vamos a asomarnos a la madriguera para ver un pequeño trozo del este extenso mundo.
Empezamos:
Funciones
Definición
Una función es una relación entre dos variables a las que, en general, llamaremos x e y.
Esta es la función que define el crecimiento de Alicia:
Esta función que define el crecimiento de Alicia:
x es la variable independiente (en el ejemplo de alicia el tiempo).
y es la variable dependiente (en el ejemplo la altura de Alicia).
La función asocia a cada valor de x un único valor de y. Se dice que y es función de x, lo que se escribe y = f(x)
Contiene tambien:
Esta es la función que define el crecimiento de Alicia:
Esta función que define el crecimiento de Alicia:
x es la variable independiente (en el ejemplo de alicia el tiempo).
y es la variable dependiente (en el ejemplo la altura de Alicia).
La función asocia a cada valor de x un único valor de y. Se dice que y es función de x, lo que se escribe y = f(x)
Contiene tambien:
Contiene tambien:
Máximo absoluto
Una función tiene su máximo absoluto en el x = a si la ordenada es mayor o igual que en cualquier otro punto del dominio de la función.
Mínimo absoluto a = 0
Una función tiene su mínimo absoluto en el x = b si la ordenada es menor o igual que en cualquier otro punto del dominio de la función.
Máximo y mínimo relativo b = 0
Una función f tiene un máximo relativo en el punto a, si f(a) es mayor o igual que los puntos próximos al punto a.
Una función f tiene un mínimo relativo en el punto b, si f(b) es menor o igual que los puntos próximos al punto b.
Una función tiene su máximo absoluto en el x = a si la ordenada es mayor o igual que en cualquier otro punto del dominio de la función.
Mínimo absoluto a = 0
Una función tiene su mínimo absoluto en el x = b si la ordenada es menor o igual que en cualquier otro punto del dominio de la función.
Máximo y mínimo relativo b = 0
Una función f tiene un máximo relativo en el punto a, si f(a) es mayor o igual que los puntos próximos al punto a.
Una función f tiene un mínimo relativo en el punto b, si f(b) es menor o igual que los puntos próximos al punto b.
Tipos de funciones
Dependiendo de ciertas características que tome la expresión algebraica o notación de la función f en x, tendremos distintos tipos de funciones:
Función constante
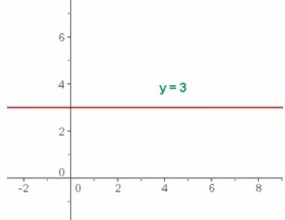
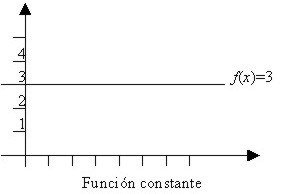
Una función de la forma f(x) = b, donde b es una constante, se conoce como una función constante.
Por ejemplo, f(x) = 3, (que corresponde al valor de y) donde el dominio es el conjunto de los números reales y el recorrido es {3}, por tanto y = 3. La gráfica de abajo muestra que es una recta horizontal.
Función lineal
Una función de la forma f(x) = mx + b se conoce como una función lineal, donde m representa la pendiente y b representa el intercepto en y. La representación gráfica de una función lineal es una recta. Las funciones lineales son funciones polinómicas.
Ejemplo:
f(x) = 2x − 1
es una función lineal con pendiente m = 2 e intercepto en y en (0, −1). Su gráfica es una recta ascendente.
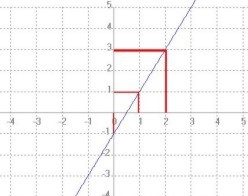
f(x) = 2x − 1
En general, una función lineal es de la forma
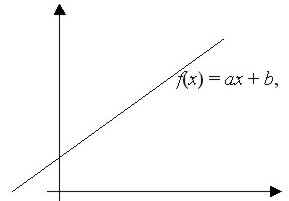
f(x) = ax + b, donde a y b son constantes (la a es lo mismo que la m anterior (corresponde a la pendiente).
Para trazar la gráfica de una función lineal solo es necesario conocer dos de sus puntos.
La ecuación matemática que representa a esta función, como ya vimos, es f(x) = ax + b, donde f(x) corresponde al valor de y, entonces
y = ax + b
Donde “a” es la pendiente de la recta, y “b” es la ordenada al origen.
La pendiente indica la inclinación de la recta, cuanto sube o baja y cuanto avanza o retrocede. Esto depende del signo que tenga.
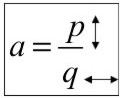El valor de “a” siempre es una fracción (si no tiene nada abajo, es porque tiene un 1), donde el numerador (p) me indica cuanto sube o baja, y el denominador (q) indica cuanto avanzo o retrocedo.
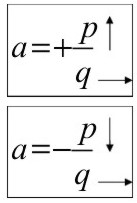
Aprendido esto, y según el signo de la fracción, la pendiente se marca de la siguiente forma
La ordenada al origen (b) es el valor donde la recta corta al eje y.
La recta siempre va a pasar por el punto (0; b)
Dependiendo de ciertas características que tome la expresión algebraica o notación de la función f en x, tendremos distintos tipos de funciones:
Función constante
Una función de la forma f(x) = b, donde b es una constante, se conoce como una función constante.
Por ejemplo, f(x) = 3, (que corresponde al valor de y) donde el dominio es el conjunto de los números reales y el recorrido es {3}, por tanto y = 3. La gráfica de abajo muestra que es una recta horizontal.
| |
Función lineal
Una función de la forma f(x) = mx + b se conoce como una función lineal, donde m representa la pendiente y b representa el intercepto en y. La representación gráfica de una función lineal es una recta. Las funciones lineales son funciones polinómicas.
Ejemplo:
f(x) = 2x − 1
es una función lineal con pendiente m = 2 e intercepto en y en (0, −1). Su gráfica es una recta ascendente.
|
| f(x) = 2x − 1 |
En general, una función lineal es de la forma
|
| f(x) = ax + b, donde a y b son constantes (la a es lo mismo que la m anterior (corresponde a la pendiente). |
Para trazar la gráfica de una función lineal solo es necesario conocer dos de sus puntos.
La ecuación matemática que representa a esta función, como ya vimos, es f(x) = ax + b, donde f(x) corresponde al valor de y, entonces
y = ax + b
Donde “a” es la pendiente de la recta, y “b” es la ordenada al origen.
La pendiente indica la inclinación de la recta, cuanto sube o baja y cuanto avanza o retrocede. Esto depende del signo que tenga.
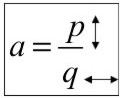
El valor de “a” siempre es una fracción (si no tiene nada abajo, es porque tiene un 1), donde el numerador (p) me indica cuanto sube o baja, y el denominador (q) indica cuanto avanzo o retrocedo.
Aprendido esto, y según el signo de la fracción, la pendiente se marca de la siguiente forma
La ordenada al origen (b) es el valor donde la recta corta al eje y.
La recta siempre va a pasar por el punto (0; b)
Representación gráfica de una función lineal o función afín
Para graficar una recta, alcanza con los datos que da la ecuación matemática de la función, y se opera de la siguiente manera:
1. Se marca sobre el eje y la ordenada al origen, el punto por donde la recta va a cortar dicho eje.
2. Desde ese punto, subo o bajo según sea el valor de “p” y avanzo o retrocedo según indique el valor de “q”. En ese nuevo lugar, marco el segundo punto de la recta.
3. Se podría seguir marcando puntos con la misma pendiente, pero con 2 de ellos ya es suficiente como para poder graficar la recta.
4. Teniendo ya los dos puntos, con regla se traza la recta que pasa por los mismos.
Para graficar una recta, alcanza con los datos que da la ecuación matemática de la función, y se opera de la siguiente manera:
1. Se marca sobre el eje y la ordenada al origen, el punto por donde la recta va a cortar dicho eje.
2. Desde ese punto, subo o bajo según sea el valor de “p” y avanzo o retrocedo según indique el valor de “q”. En ese nuevo lugar, marco el segundo punto de la recta.
3. Se podría seguir marcando puntos con la misma pendiente, pero con 2 de ellos ya es suficiente como para poder graficar la recta.
4. Teniendo ya los dos puntos, con regla se traza la recta que pasa por los mismos.
No hay comentarios:
Publicar un comentario